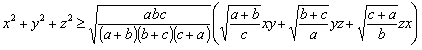曹杨二中度第一学期期中考试高中一年级数学试题
1、填空题
1.设全集![]() 则
则![]() _______.
_______.
2.满足![]() 的集合M的个数是________.
的集合M的个数是________.
3.设![]() 若
若![]() 是
是![]() 的充分条件,则
的充分条件,则![]() 的取值范围为_______.
的取值范围为_______.
4.已知![]() 命题“若
命题“若![]() 则
则![]() ”的否命题是______________.
”的否命题是______________.
5.函数![]() 的概念域是__________.
的概念域是__________.
6.若![]() 则
则![]() _________.
_________.
7.已知![]() 则
则![]() 的最大值是_______.
的最大值是_______.
8.已知正实数![]() 满足
满足![]() 则
则![]() 的最小值为_________.
的最小值为_________.
9.若关于![]() 的不等式
的不等式![]() 的解集为
的解集为![]() 则关于
则关于![]() 的不等式
的不等式
![]() 的解集是___________.
的解集是___________.
10.二次函数![]() 的图像与
的图像与![]() 轴的两个交点的横坐标分别为
轴的两个交点的横坐标分别为![]() 且
且
![]() 则
则![]() 的取值范围是_________.
的取值范围是_________.
11.设![]() 的概念域是
的概念域是![]() 则函数
则函数![]() 的概念域为_______.
的概念域为_______.
12.概念满足不等式![]() 的实数
的实数![]() 的集合叫做A的B范围,若
的集合叫做A的B范围,若![]() 的
的![]() 范围是一个关于原点对称的区间,则
范围是一个关于原点对称的区间,则![]() 的最小值为_________.
的最小值为_________.
2、选择题
13.设集合![]() 则
则
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
14.设命题甲为“![]() ”,命题乙为“
”,命题乙为“![]() ”,那样甲是乙的
”,那样甲是乙的
A.充分而非必要条件 B.充分必要条件
C.必要而不充分条件 D.既不充分也非必要条件
15.函数![]() 则对任意实数
则对任意实数![]() ,下列不等式总成立的是
,下列不等式总成立的是
A.![]() B.
B.![]()
C.![]() D.
D.![]()
16.对于使![]() 成立的所有常数中,大家把M的最小值1叫做
成立的所有常数中,大家把M的最小值1叫做![]() 的上确界,若
的上确界,若![]() 且
且![]() ,则
,则![]() 的上确界为
的上确界为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3、解答卷
17.记关于![]() 的不等式
的不等式![]() 的解集为P,不等式
的解集为P,不等式![]() 的解集为Q,若
的解集为Q,若
![]() 求实数
求实数![]() 的取值范围。
的取值范围。
18.若实数![]() 满足
满足![]() 则称
则称![]() 比
比![]() 离得远远的
离得远远的![]()
若![]() 比
比![]() 离得远远的0,求
离得远远的0,求![]() 的取值范围;
的取值范围;
对任意两个不相等的正实数![]() 证明:
证明:![]() 比
比![]() 离得远远的
离得远远的![]()
19.为了减少能源损耗,近期上海对新建住宅的屋顶和外墙都需要建造隔热层,某幢建筑物要建造可用20年的隔热层,每厘米的隔热层建导致本为6万元,该建筑物每年的能源损耗成本C与隔热层厚度![]() 满足关系:
满足关系:![]() 若不建隔热层,每年能源损耗成本为8万元,设
若不建隔热层,每年能源损耗成本为8万元,设![]() 为隔热层建造成本与20年的能源损耗成本之和.
为隔热层建造成本与20年的能源损耗成本之和.
求![]() 的值及
的值及![]() 的表达式;
的表达式;
隔热层修建多厚时,总成本![]() 达到最小,并求最小值。
达到最小,并求最小值。
20.已知一元二次函数![]() 的图像与
的图像与![]() 轴有两个不一样的交点,其中一个交点的坐标为
轴有两个不一样的交点,其中一个交点的坐标为![]() 且当
且当![]() 时,恒有
时,恒有![]()
求出不等式![]() 的解;
的解;
若以二次函数的图像与坐标轴的三个交点为顶点的三角形的面积为8,求![]() 的取值范围;
的取值范围;
若不等式![]() 对所有
对所有![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围。
的取值范围。
附加题
21.设![]() 且
且![]() 是E的真子集,且G具备下列两条性质:
是E的真子集,且G具备下列两条性质:
对任何![]() 恒有
恒有![]()
![]()
试证:G中的奇数的个数是4的倍数,且G中的所有数字的平方和为肯定数
22.设![]() 试证:对任意实数
试证:对任意实数![]() 有
有